Visualisering av undersökningsmaterialet
Det är viktigt att kunna presentera sifferuppgifter åskådligt och lättförståeligt. Kvantitativ kunskap samlas exempelvis in om ekonomin i företag och samfund, om miljöns tillstånd, idrott, samhällelig verksamhet, politiska åsikter och tekniska apparaters egenskaper. Influencers följer med antal följare och tittare medan bilens instrumentbräda ger information om hastigheten, motorns temperatur och bensinmängden.
Information i sifferform är exakt, men om den visas på ett misslyckat sätt kan den leda till förvirring och missförstånd. Man behöver dock bara kasta ett öga på en välgjord bild för att se de relevanta kvantitativa uppgifterna.
På samma sätt som man ändrar, sammanfattar, förkortar och förtydligar en text borde man också fila på presentationsformen för numeriska uppgifter så länge att frågans kärna tydligt syns. De vanligaste digitala verktygens standardpresentationer för visuellt innehåll är förvånansvärt dåliga, så också andra än proffsgrafiker har nytta av att lära sig de bästa grundtricksen.
Ovanstående sortens högstämda principförkunnelser förblir oftast svävande på begreppsnivå. Därför ska jag ge två handgripliga exempel. I det första ger jag er resultaten från Finlands riksdagsval 1991 och 1995 i formen av ett stapeldiagram. I det andra ska jag jämföra vintrarna under 1970-talet med de senaste årens vintrar.
För det mesta använder jag Matlab för att skapa sådan här infografik. Det är ett professionellt program för matematiker och statistiker. Eftersom det är en dyr produkt som alla inte har tillgång till ska jag skapa nedanstående exempel med Microsofts PowerPoint och Excel. Det finns också gratisverktyg på webben, såsom Google Charts, LibreOffice (eller Charts) och många andra. Man kan få samma slutresultat med vilket som helst av dessa verktyg. Huvudsaken är att man själv funderar på hur man tydligast kan presentera uppgifterna och sedan leker man med softan tills det lyckas.
Resultaten i riksdagsvalen 1991 och 1995
Låt oss först titta på valet 1991. Wikipediaartikeln om riksdagsvalet hänvisar till Statistikcentralens öppet tillgängliga data, enligt vilka rösterna fördelades så här:
| Parti | Röstandel |
|---|---|
| Centern i Finland | 24,8 |
| Finlands socialdemokratiska parti | 22,1 |
| Nationella Samlingspartiet | 19,3 |
| Vänsterförbundet | 10,1 |
| Gröna förbundet | 6,8 |
| Svenska folkpartiet | 5,5 |
| Finlands landsbygdsparti | 4,9 |
| Finlands kristliga förbund | 3,1 |
| Liberala folkpartiet | 0,8 |
| Övriga | 2,6 |
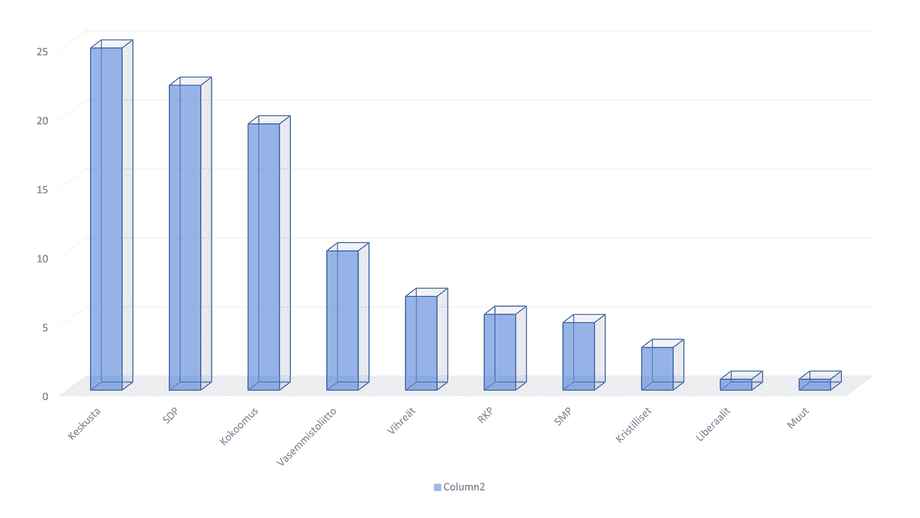
Om det bara finns ett fåtal siffror som ska presenteras är det oftast mest effektivt och tydligast att använda en tabell. I vårt exempel finns det tio sifferuppgifter och då kan det vara motiverat att använda en visuell presentationsform. Jag väljer PowerPoint som verktyg eftersom det erbjuder ett färdigt alternativ för detta:
Den här presentationsformen behöver piffas upp lite. Största problemet är att den konstgjorda tredimensionella formen är helt onödig och gör det svårt att exakt bedöma vilken procentandel som respektive parti fått. På toppen av staplarna finns det ett virrvarr av streck som gör det svårt att avläsa det exakta talet. Dessutom är siffrorna på den vänstra lodräta axeln på grund av den skenbara tredimensionella effekten placerade lägre ner än de vågräta strecken som de borde hänvisa till. Partinamnen har på grund av utrymmesbrist skrivits på snedden med en alldeles för liten font och det gör det också svårläst. Under diagrammet svävar en alldeles obegriplig text, ”Column 2” som inte hjälper läsaren.
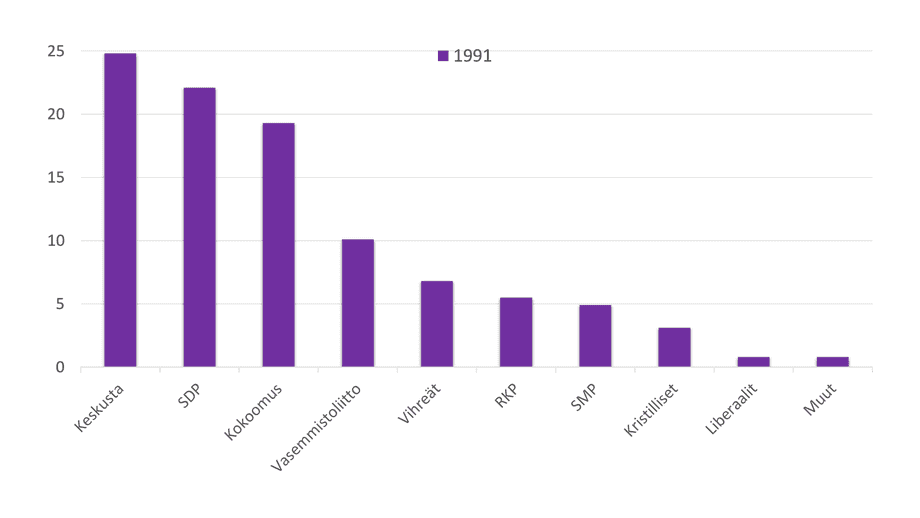
Jag byter till en tvådimensionell modell och gör staplarna enfärgade. Nu syns datan bättre och det går att avläsa hur stort stöd partierna fått.
Nu kan man jämföra partistödet. Jag förstorade också fonten. Det finns ännu utvecklingsbehov: partinamnen är fortfarande skrivna på snedden.
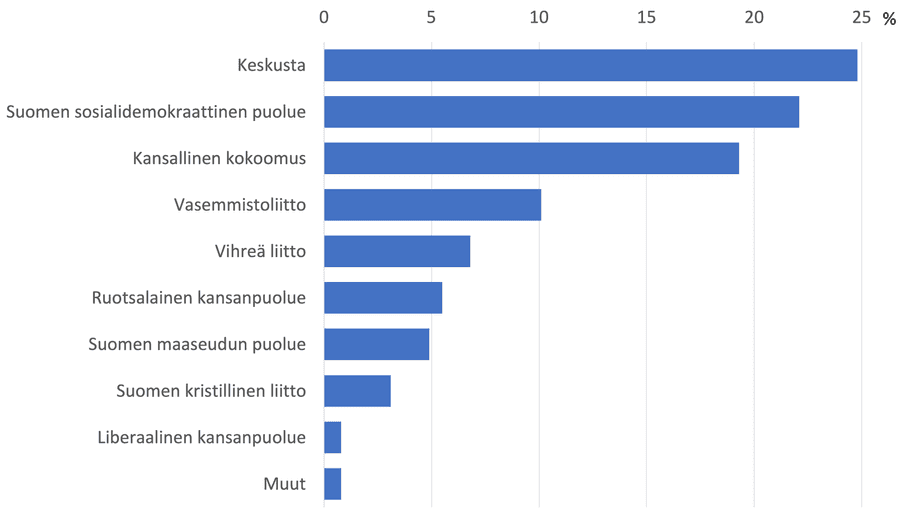
Genom att vända på staplarna så de blir vågräta ryms partiernas officiella namn också vågrätt. Nu har jag fått ihop en relativt tydlig presentation av valresultaten år 1991.
Hur gör vi om vi skulle vilja jämföra två val med varandra, till exempel valen 1991 och 1995? Då är det lite klumpigt att använda en tabell, även om det ibland kan vara det bästa alternativet. Ur en synskadad läsares synvinkel är en tabell mycket mer tillgänglig än ett visuellt diagram.
| Parti | Osuus äänistä, vuonna 1991 | Osuus äänistä, vuonna 1995 |
|---|---|---|
| Centern i Finland | 24,8 | 19,9 |
| Finlands socialdemokratiska parti | 22,1 | 28,3 |
| Nationella Samlingspartiet | 19,3 | 17,9 |
| Vänsterförbundet | 10,1 | 11,2 |
| Gröna förbundet | 6,8 | 6,5 |
| Svenska folkpartiet | 5,5 | 5,1 |
| Finlands landsbygdsparti | 4,9 | 1,3 |
| Finlands kristliga förbund | 3,1 | 3 |
| Liberala folkpartiet | 0,8 | 0,6 |
| Ungfinska partiet | - | 2,8 |
| Övriga | 2,6 | 3,4 |
Eftersom det i det här fallet handlar om hur man visualiserar data ska vi förvandla den dubbla tabellen till en bild.
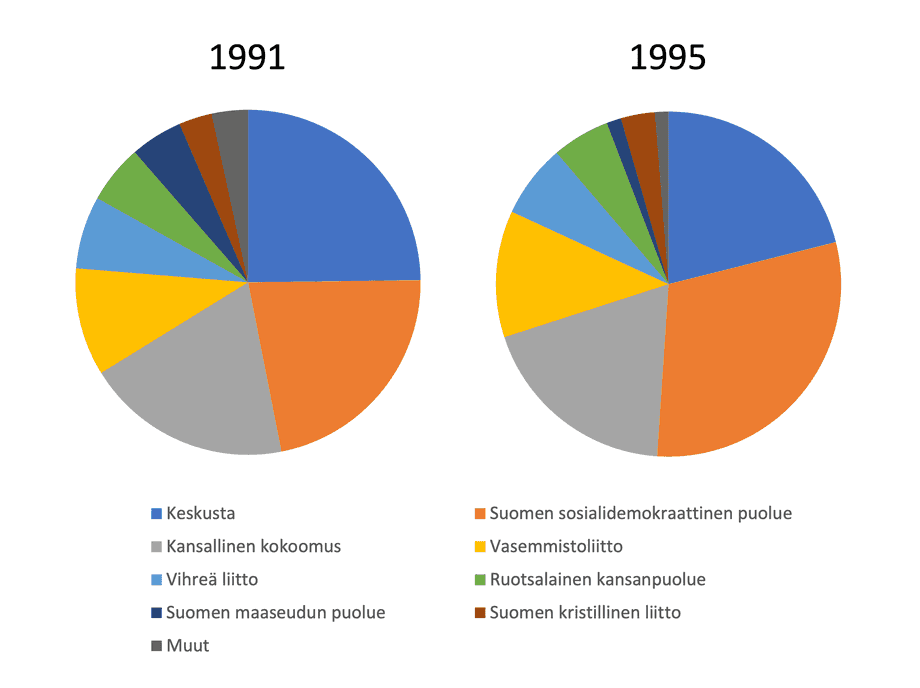
Cirkeldiagram används ofta när man vill visa hur hundra procent fördelar sig. Ibland kan man se tårtdiagram sida vid sida, så här:
Att visa flera cirkeldiagram är ett dåligt sätt att presentera numeriska data på. Försök till exempel titta på cirkeldiagrammen och berätta för mig om SFP fick en större procentuell andel av rösterna år 1991 eller år 1995? Eller kan du berätta vem som vann och med vilken marginal år 1991?
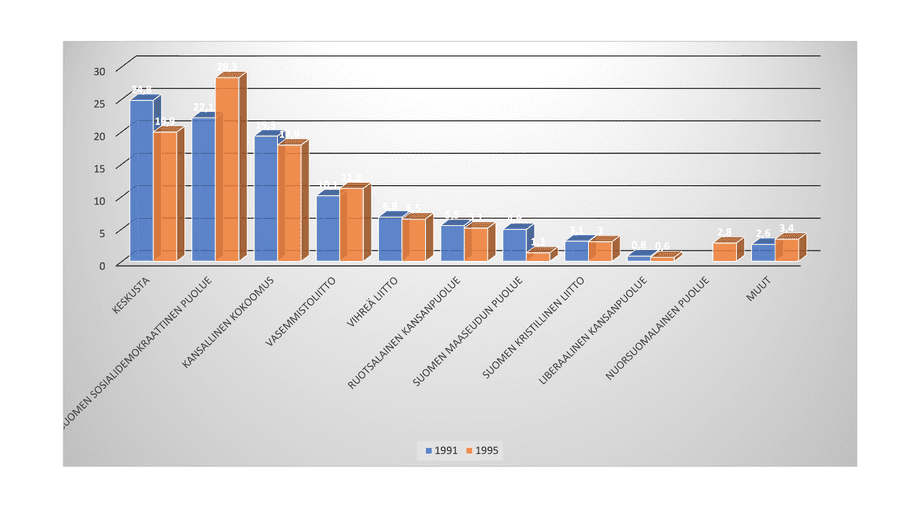
Vi återgår till stapeldiagrammet som tjänade vårt syfte väl när det gällde ett val. PowerPoint gör det möjligt att inkludera flera dataserier, men det är en bra idé att kolla vilken standardinställning som valts.
Än en gång stör den konstgjorda tredimensionella effekten uppgifterna. På köpet erbjuder PowerPoint också en helt onödig genomskinlig effekt och placerar procentandelarna i vita siffror uppe på staplarna, vilket gör dem omöjliga att läsa.
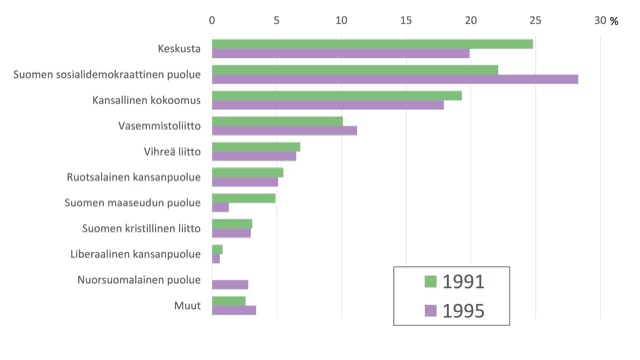
I ett slag förbättrade jag presentationsformen. Nu kan vi enkelt jämföra talen och procentandelarna presenteras tydligt och klart. Färgkartan plockade jag på webbplatsen ColorBrewer 2.0, där jag valde en karttyp som skiljer på färgerna (diverging). Jag såg också till att färgblinda kan skilja färgerna från varandra genom att välja colorblind safe. Dessutom valde jag den trygga utskriftinställningen print friendly. Färgkartans ytterligheter grönt och violett är perfekta färger för dubbla staplar. Jag försäkrade mig ännu om saken genom att mata in bilden i Coblis färgblindhetssimulator. Enligt den kan alla som lider av någon form av färgblindhet, förutom den ovanliga formen akromatopsi, urskilja färgerna på staplarna.
Var det kallare förr om vintrarna?
Jag var barn under 1970-talet och jag brukar trötta ut mina vänner med att tjata om hur ordentliga vintrar vi hade då. Eftersom Meteorologiska institutet har en utomordentlig tjänst med öppna data (på finska) kan vi nu enkelt kontrollera om mitt påstående stämmer.
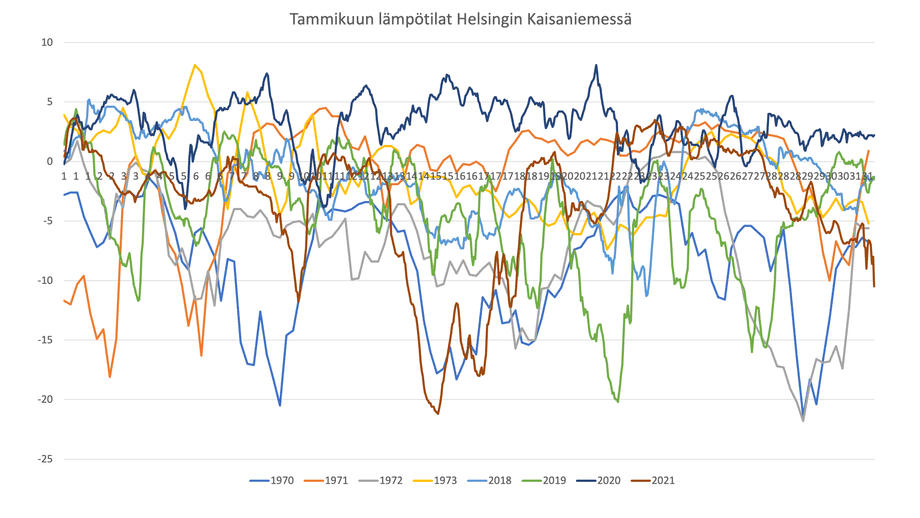
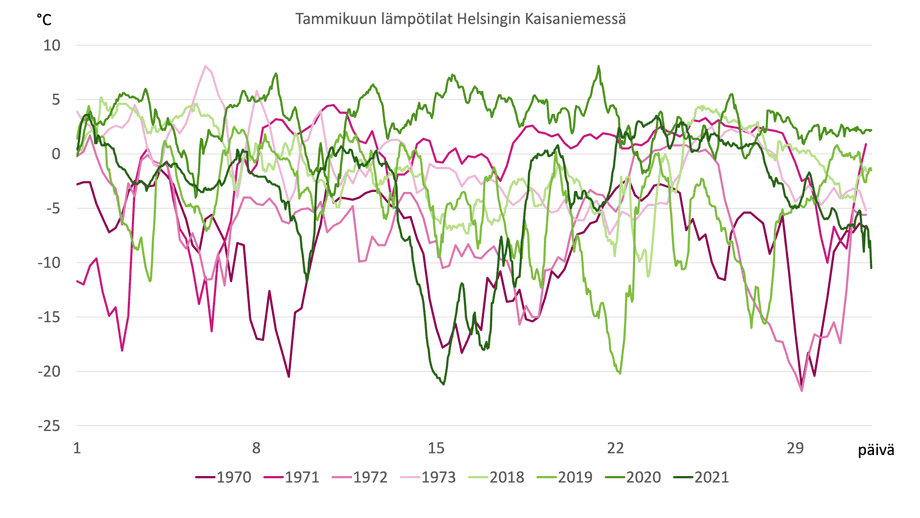
Denna grafik visar hur temperaturen växlat under januari i Helsingfors centrum de fyra senaste åren samt i början av 1970-talet.
Den här spagettin är omöjlig att förstå sig på utan att man riktigt sätter sig in i det hela och knappt ens då. Hur skulle vi kunna förtydliga bilden? Och framför allt: kan vi med en och samma bild visa alla dessa numeriska data och dra en tydlig slutsats om hur vintrarna eventuellt har förändrats under fem årtionden?
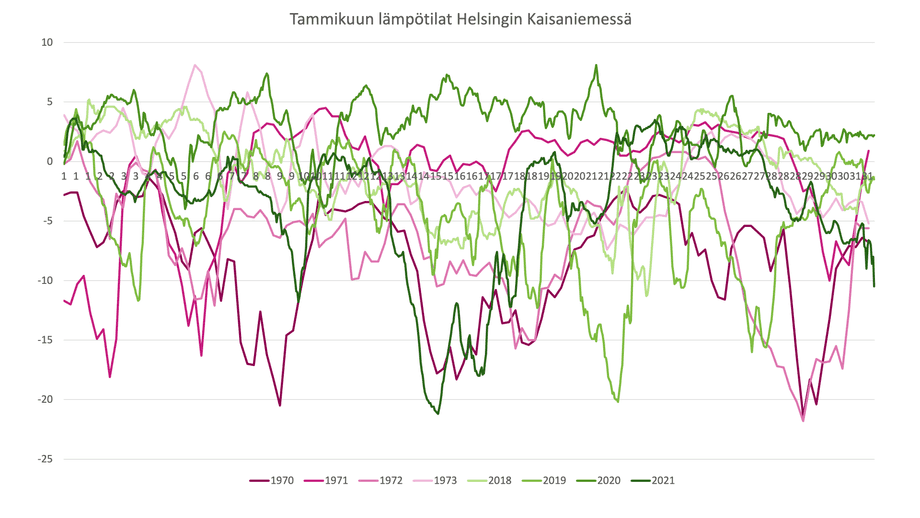
Jag använder verktyget ColorBrewer 2.0 och plockar ut färgnyanser som skiljer sig åt för de två kategorierna genom att välja färgkartstypen diverging color scheme. Jag kontrollerar att färgerna skiljer sig åt och är lämpliga också för färgblinda genom att klicka på colorblind safe. Färgnyanserna syns som koder, till exempel i HEX- eller RGB-form, och går då att mata in i PowerPoint som färger för kurvan. Det här är lite småpetigt, men det är det värt!
Kurvorna i violetta nyanser representerar 1970-talet medan de gröna kurvorna visar nyare väderuppgifter.
Jag förstorar också fonten och tillägger information om mätenheten, alltså dag och celsiusgrader, vid den vågräta och lodräta axeln.
Även om bilden blev tydligare med dessa färgval och övriga förändringar är det fortfarande svårt att jämföra vintrarna förr och nu. Hur skulle jag ytterligare kunna förenkla det för läsaren?
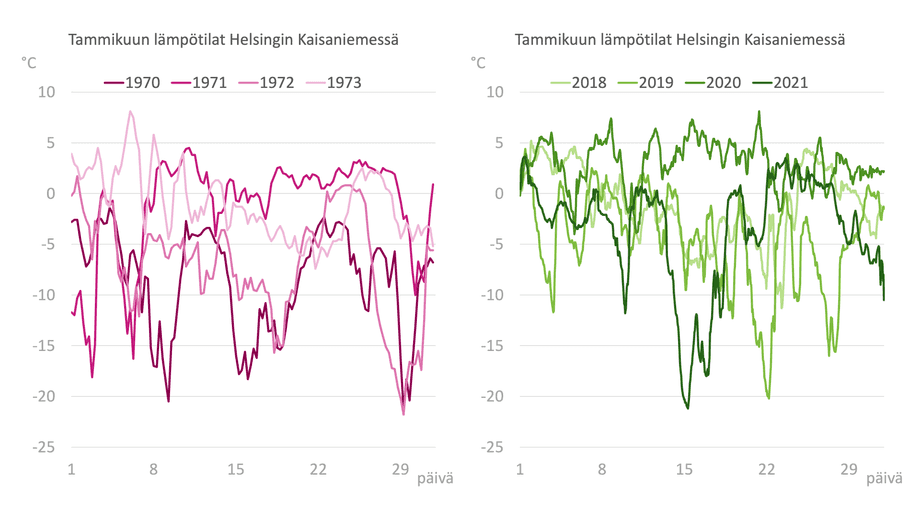
Ett av de mest effektiva sätten att presentera nummeruppgifter visuellt är att placera samma strukturer bredvid varandra med omsorgsfullt valda skillnader i datamaterialet. Jag sätter väderuppgifterna för år 1970 i en egen liten bild till vänster och de nya uppgifterna till höger. En viktig detalj är att diagrammen ska vara exakt lika stora och att de vågräta och lodräta axlarna ska ha samma skala. Då kan man göra en jämförelse där skillnaderna mellan siffrorna spelar huvudrollen.
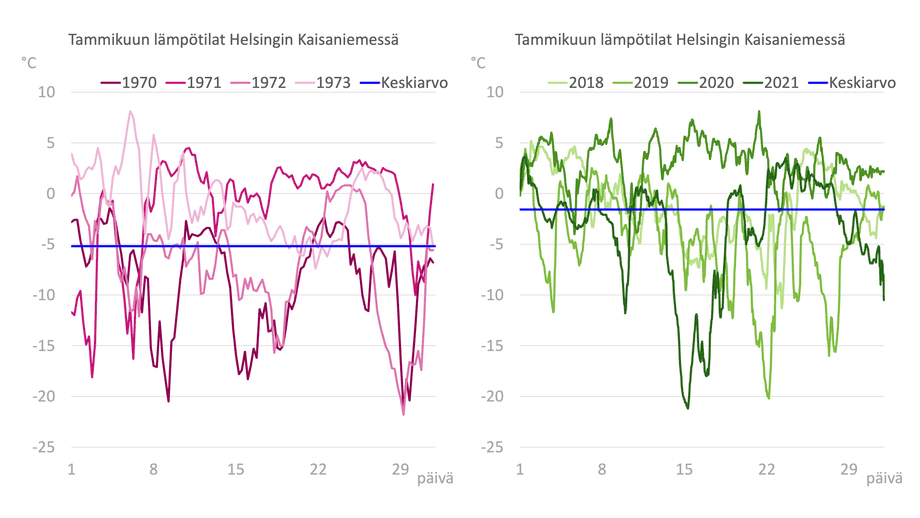
Kanske de där gröna trådarna faktiskt når lite högre upp än de violetta, men är det möjligt att dra några slutsatser om varmare vintrar utifrån detta? Nu ska vi hjälpa blicken genom att tillsätta ett vågrätt blått streck i båda figurerna. Det visar medelvärdet.
Medelvärdet för de fyra första januarimånaderna under 1970-talet är -5,2 grader. Motsvarande medelvärde för de fyra senaste januarimånaderna är -1,6 grader.
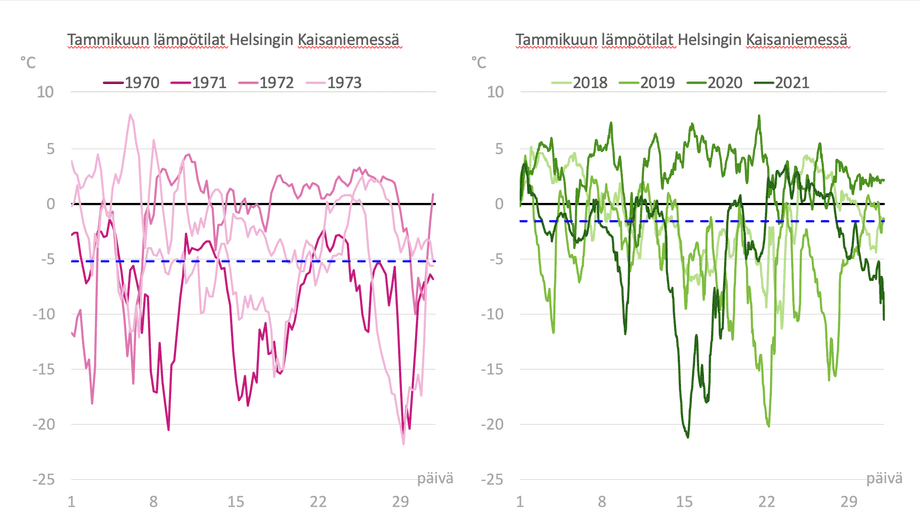
En av mina försökspersoner påpekade att hen trodde att den blå linjen innebar 0 grader när hen kastade en snabb blick på figurerna. Jag gjorde mig alltså skyldig till misstaget jag nämnde i början, nämligen att jag gömde strukturen för mycket under datan. Jag korrigerar läget genom att rita ut nollnivån med ett vågrätt streck så man tydligt ser att gradskalorna på de båda bilderna motsvarar varandra. På samma gång byter jag ut linjen som visar medelvärdet till en streckad linje. Nu är jag nöjd, även om man säkert kunde förbättra bilden ännu mer. Men man måste också kunna sluta i tid.
Utifrån detta bildpar kan man alltså anta att vintrarna nuförtiden är betydligt mycket varmare än de var för 50 år sedan. Liksom det ofta går när man presenterar numeriska data är det inte riktigt så här enkelt. Om jag till den vänstra bilden i stället hade valt åren 1972–1975 så skulle medeltemperaturen ha varit -2,5 grader. Och om jag till den högra bilden hade valt temperaturerna 2010–2013 så hade vi fått medeltemperaturen -5,8 grader. Då skulle det se ut som om vintrarna har blivit kallare.
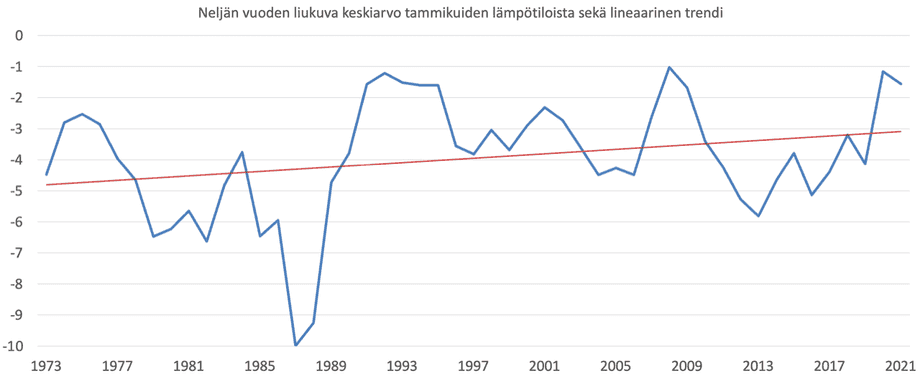
Vi kan få klarhet i detta genom att rita ut ett glidande medelvärde för de fyra åren.
Värdet vid 1973 på den här bilden avser alltså medeltemperaturen i januari under åren 1969–1973 och vid 2021 finns medeltemperaturen för januari under åren 2018–2021. Vid vartdera året finns alltså ett medelvärde för det året och de tre föregående åren: det här är detsamma som ett glidande medelvärde. Notera att det finns en topp år 1975 och en dal år 2013. Vid de åren plockade jag exemplet ovan som visar att det blivit kallare.
Och nu kan vi besvara min ursprungliga fråga. Jag sätter in en lineär trend i rött på den där krängande blå kurvan. Den visar temperaturens huvudsakliga beteende under granskningsperioden. Så sant som det är sagt: vintrarna har i medeltal blivit mildare, även om vädrets årliga växlingar (och till och med under fyra år) är kraftiga i Finland.